Numeri Complessi

Analisi #Incompleto

Definizione

• I numeri complessi sono una estensione dei numeri reali - $\mathbb{R}\subset \mathbb{C}$
• Nell’insieme dei numeri complessi è possibile estrarre le radici ad indice pari di numeri negativi e risolvere le equazioni di secondo grado con discriminante negativo

Estensione dei numeri Reali

In $\mathbb{R}$ è impossibile trovare le soluzioni dell’equazioni secondo grado:

$$x^2+1=0⟺x_{2}2=-1$$

Da qua si può introdurre l’unità immaginaria, definita come la radice quadrata di -1

$$i:=\sqrt{-1}$$

In questo modo l’equazione $x^2+1=0$ ammette soluzioni, in particolare ammette due radici complesse distinte $x_1=i$ e $x_2=-i$

$$\begin{array}{rl}& x^2+1=0\\ & x^2=-1\\ & x=\pm \sqrt{-1}\\ & x=\pm i\end{array}$$

Introdotta l’unità immaginaria si può definire l’insieme dei numeri complessi come l’insieme di tutti e soli i numeri della forma $a+ib$ con $a,b\in \mathbb{R}$

Forma Algebrica

Parte reale e immaginaria

Sia $z=a+ib$ un qualsiasi numero complesso, con $a,b\in \mathbb{R}$

• Il numero $a$ è il numero reale e si indica con $\mathrm{Re}(z)$
• Il numero $ib$ è il numero immaginario e si indica con $\mathrm{Im}(z)$

$$z=a+ib\{\begin{array}{l}\mathrm{Re}(z)=a\text{parte reale}\\ \mathrm{Im}(z)=b\text{parte immaginaria}\end{array}$$

Piano di Argand-Gauss

Per i numeri complessi è possibile individuare una corrispondenza biunivoca tra gli elementi dell’insieme $\mathbb{C}$ e i punti del piano, detto piano complesso o piano di Argand-Gauss.

Al numero complesso $z=a+ib$ si associa il punto del piano di coordinate cartesiane $(a,b)=(\mathrm{Re},\mathrm{Im})$

$$a+ib⟺(a,b)$$

In pratica, il piano di Argand-Gauss è un piano cartesiano leggermente modificato in cui l’asse x è chiamata asse reale e l’asse y è detto asse immaginario

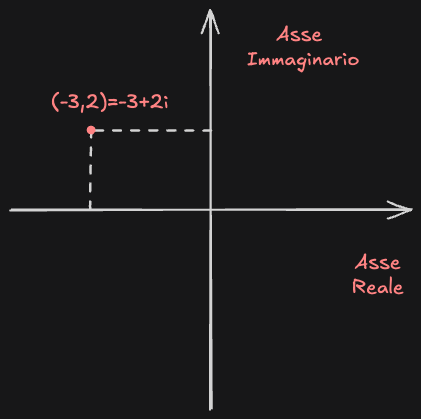
Numeri complessi come coppia ordinata

Possiamo definire l’insieme dei numeri complessi $\mathbb{C}$ come l’insieme ottenuto dal prodotto cartesiano di $\mathbb{R}$ con se stesso

$$\mathbb{C}:=\mathbb{R}\times \mathbb{R}={\mathbb{R}}^2=\{(a,b)|a,b\in \mathbb{R}\}$$

ne segue che ogni numero complesso è una coppia ordinata di numeri reali, ossia:

$$z\in \mathbb{C}⟺z=(a,b)\text{con}a,b\in \mathbb{R}$$

I numeri complessi della forma $(a,0)$ coincidono con i numeri reali, mentre i numeri del tipo $(0,b)$ sono gli immaginari puri

L’unita immaginaria $i$ è il numero complesso immaginario pure che si identifica con la coppia ordinata $i=(0,1)$

Di seguito la definizione della somma e prodotto di due numeri complessi $z=(a,b)$ e $w=(c,d)$:

$$\begin{array}{rl}& z+w=(a,b)+(c,d)=(a+c,b+d)\\ & zw=(a,b)(c,d)=(ac-bd,bc+ad)\end{array}$$

Elemento neutro, opposto, inverso di un numero complesso

1. L’elemento neutro rispetto alla somma è $(0,0)$
2. L’opposto del numeri complesso $(a,b)$ è $(-a,-b)$
3. L’elemento neutro rispetto al prodotto è $(1,0)$
4. L’inverso moltiplicativo di $z=(1,b)\ne (0,0)$ è

$$z^{-1}=(\frac{a}{a^2+b^2},\frac{-b}{a^2+b^2})$$

5. Dato $z=(a,b)$, si definisce complesso coniugato di $z$ e si indica con $\overline{z}$ il numero complesso:

$$\overline{z}=(a,-b)$$

Forma Trigonometrica

La forma trigonometrica/forma polare di un numero complesso permette la rappresentazione di un qualsiasi numero complesso mediante due valori detti modulo e argomento nella forma:

$$z=r[\cos (\theta )+i+\sin (\theta )]$$