Le Matrici

Geometria #Incompleto

Cosa è una matrice

Una matrice è una tabella in ui sono riportati in modo ordinato gli elementi di un dato insieme, generalmente sono numeri ma possono essere anche vettori o funzioni

$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ a_{m_1}& a_{m2}& \dots & a_{mn}\end{array}\right)$$ $$\left(\begin{array}{ccc}1& 2& 3\\ 3& 4& 5\end{array}\right)$$

Ogni elemento ha una posizione specifica che viene indicata con $a_{ij}$.

Dimensione di una matrice

La dimensione di una matrice è semplicemente il prodotto tra il numero di righe e di colonne di essa. Una matrice contenente numeri reali e grande $m\cdot n$ si dice che appartiene a ${\mathbb{R}}^{m\cdot n}$ .

Tipi di matrici

Matrici colonna/Vettore colonna

Matrice formata da una sola colonna

$$\left(\begin{array}{c}-3\\ 5\\ 3\\ 0\\ 7\end{array}\right)\in {\mathbb{R}}^{2,3}$$

Matrice rettangolare

Matrice in cui il numero delle righe è diverso dal numero delle colonne

Matrice quadrata

Matrice in cui il numero delle righe è uguale al numero delle colonne. La grandezza si dice ordine (es: ordine 2, ordine 4). Molto importante dato che sono le uniche che permettono di calcolare il determinante e cercare la matrice inversa.

Nelle matrici quadrate si dice:

• Diagonale principale, la diagonale che va dall’angolo in alto a sinistra a quello in basso a destra
• Diagonale secondaria: la diagonale che va dall’angolo in alto a destra a quello in basso a sinistra

Matrice diagonale

Matrice quadrata in cui gli elementi sono tutti nulli ad eccezione di quelli posti sulla diagonale principale.

Matrice antidiagonale

Come la diagonale ma gli elementi sono nulli ad eccezione di quelli sulla diagonale secondaria

Matrice identità

Matrice diagonale con tutti i valori a 1

$$\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

Matrice triangolare

Matrice quadrata avente tutti gli elementi al di sotto della diagonale principale uguali a zero

Matrice triangola inferiore

Matrice quadrata avente tutti gli elementi al di sopra della diagonale principale uguali a zero

Operazione tra matrici

Somma tra matrici

Per sommare due matrici esse devono essere della stesso tipo ($m$ righe e $n$ colonne uguali). La somma tra due matrici restituisce una nuova matrice $A+B$ che deriva dalla somma degli elementi della stessa posizione.

$$A+B=\left(\begin{array}{ccc}{a}_{11}+b_{11}& a_{12}+b_{12}& a_{13}+b_{13}\\ a_{21}+b_{21}& a_{22}+b_{22}& a_{23}+b_{23}\\ a_{31}+b_{31}& a_{32}+b_{32}& a_{33}+b_{33}\end{array}\right)$$ $$s_{ji}=a_{ji}+b_{ji},\text{ con }i\in \{1,2,\dots ,m\},i\in \{1,2,\dots ,n\}$$

Matrice opposta

Una matrice opposta -A è una matrice derivante da A ma con gli elementi opposti.

$$\begin{array}{rl}& A=\left(\begin{array}{ccc}1& 2& -3\\ -3& 4& -5\end{array}\right)\\ & \\ & -A=\left(\begin{array}{ccc}-1& -2& 3\\ 3& -4& 5\end{array}\right)\end{array}$$

Prodotto di una matrice per uno scalare

Il prodotto di una matrice per un valore scalare è abbastanza semplice, basta moltiplicare ogni elemento della matrice per il valore scalare.

$$\begin{array}{rl}& A=\left(\begin{array}{ccc}1& 2& -3\\ -3& 4& -5\end{array}\right)\text{ e }\lambda =2\\ & \text{ allora}\\ & \lambda A=2\left(\begin{array}{ccc}1& 2& -3\\ -3& 4& -5\end{array}\right)=\left(\begin{array}{ccc}2\cdot 1& 2\cdot 2& 2\cdot -3\\ 2\cdot -3& 2\cdot 4& 2\cdot -5\end{array}\right)=\left(\begin{array}{ccc}2& 4& -6\\ -6& 8& -10\end{array}\right)\end{array}$$

Prodotto tra matrici

Il prodotto tra matrici è possibile unicamente quando la il numero di colonne della prima matrice è uguale al numero di righe della seconda.

$$\begin{array}{rl}& A\in {\mathbb{R}}^{2,3}B\in {\mathbb{R}}^{3,4}\\ & A_i=B_j\end{array}$$

Il risultato del prodotto sarà il seguente:

$$(2,/)\cdot (/,4)=(2,4)$$

Warning

Non è possibile eseguire il prodotto di $BA$ essendo che il numero di colonne di $B$ non è uguale al numero di righe di $A$

\begin{aligned} &B(2,4) \quad A(2,3)\\ & B_{i} \neq A_{j}

\end{aligned}

Esempio

$$A=\left(\begin{array}{ccc}1& 0& 2\\ 0& 3& -1\end{array}\right)B=\left(\begin{array}{cc}4& 1\\ -2& 2\\ 0& 3\end{array}\right)$$

Il prodotto si può fare, la nuova matrice avrà 2 righe e 2 colonne. Adesso iniziamo a moltiplicare $A_{11}$ con $B_{11}$, poi $A_{12}$ con $B_{21}$ e cosi via.

$$1\cdot 4+0\cdot (-2)+2\cdot 0=4+0+0=4$$

Il risultato di queste moltiplicazioni sarà il valore dell’elemento $A{B}_{11}$ Adesso si rifà la stessa cosa con la prima riga di $A$ e la seconda colonna di $B$

$$1\cdot 1+0\cdot 2+2\cdot 3=1+0+6=7$$

Con questo abbiamo ottenuto la seconda colonna della prima riga di $AB$.

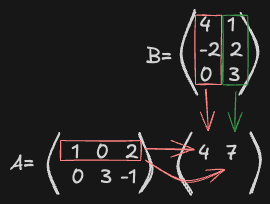
Adesso si rifanno gli stessi procedimenti ma con la seconda riga di $A$. Quindi il risultato sarà:

$$AB=\left(\begin{array}{ccc}1& 0& 2\\ 0& 3& -1\end{array}\right)\cdot \left(\begin{array}{cc}4& 1\\ -2& 2\\ 0& 3\end{array}\right)=\left(\begin{array}{cc}4& 7\\ -6& 3\end{array}\right)$$